Risk and expected return are the two key determinants of an investment decision.
Risk, in simple terms, is associated with the variability of the rates of return from an investment; how much do individual outcomes deviate from the expected value? Statistically, the risk is measured by any one of the measures of dispersion such as Coefficient of range, variance, standard deviation, etc.
The Risk involved in investment depends on various factors such as:
- The length of the maturity period–longer maturity periods impart greater risk to investments.
- The Credit-worthiness of the issuer of securities – the ability of the borrower to make periodical interest payments and pay back the principal amount will impart safety to the investment and this reduces risk.
- The nature of the instrument or security also determines the risk. Generally, government securities and fixed deposits with banks tend to be the riskless or least risky; Corporate debt instruments like the Debentures tend to be riskier than government bonds and ownership instruments like equity shares tend to be riskiest. The relative ranking of instruments by risk is once again connected to the safety of the investment.
- Equity shares are considered to be the most risky investment on account of the variability of the rates of returns and also because the residual risk of bankruptcy has to be borne by the equity holders.
- The liquidity of an investment also determines the risk involved in that investment. Liquidity of an asset refers to its quick sale ability without a loss or with a minimum of loss.
- In addition to the foretasted factors, there are also various others such as the economic, industry and firm specific factors which affect the risk an investment.
Another major factor determining the investment decision is the rate of return expected by the investor. The rate of return expected by the investor consists of the yield and capital appreciation.
Before we look at the methods of computing the rate of return from an investment, it is necessary to understand the concept of the return on investment.
We have noted earlier that an investment is a postponed consumption. Postponement of consumption is synonymous with the concept of ‘time preference for money. Other things remaining the same, individuals prefer current consumption to future consumption. Therefore, in order to induce individuals to postpone current consumption, they have to be paid a certain compensation which is the time preference for consumption. The compensation paid should be a positive real rate of return.
The Real Rate of Return is generally equal to the rate of return expected by an investor from a risk-free capital asset assuming a world without inflation. However, in real life, inflation is a common feature of a capitalist economy. If the investor is not compensated for the effects of inflation, the real rate of return may turn out to be either zero or negative. Therefore, the investors, generally, add expected inflation rate to the real rate of return to arrive at the Nominal Rate of Return.
For example, assume that the present value of an investment is Rs. 100, the investor expects a real-time rate of 3 percent per annum and the expected inflation rate is 3 percent per annum. If the investor were to receive only the real-time rate he would get back Rs. 103 at the end of one year. The real rate of return received by the investor would be equal to zero because the rime preference rate of 3% per annum is matched by the inflation of 3% per annum. If the actual inflation rate is greater than 3% annum, the investor would suffer negative returns.
Thus, the Nominal Rate of Return on a Risk-Free Asset is equal to the time preference real rate plus expected inflation rate.
If the investment is capital assets other than government obligations, such assets would be associated with a degree of risk which is idiosyncratic to the investment. For an individual to invest in such assets, an additional compensation called the Risk Premium will have to be paid over and above the nominal rate of return.
Therefore, three major determinants of the Rate of Return expected by the investor are:
- The time preference risk free real rate
- The expected rate of inflation
- The risk associated with the investment which is unique to the investment.
Hence,
Required return = Risk free real rate + Inflation premium + Risk premium
It was stated earlier that the rate of return from an investment consists of the yield and capital appreciation if any. The difference between the sale price and the purchase price is the capital appreciation and the interest or dividend divided by the purchase price is the yield. Accordingly
Rate Pf return(Rt) = It + [Pt – Pt-1] / Pt-1. ……………….. (Eqn 1)
Where
Rt = Rate of return per time period ‘t’
It = Income for the period ‘t’
Pt = Price at the end of time period ‘t’
Pt-1 = Initial price, i.e., the price at the beginning of the period ‘t’.
In the above equation ‘t’ can be a day or a week or a month or a year or years and accordingly daily, weekly, monthly or annual rates of return could be computed for most capital assets.
The above equation can be split into two components. Viz.,
Rate of return (Rt) = (It / Pt-1) + ([Pt – Pt-1] / Pt ) ……………….. (Eqn 2)
Where,
(It / Pt-1) is called the current yield, and
([Pt – Pt-1] / Pt ) is called the capital gain yield.
To illustrate, suppose the following information is given for a corporate bond:
Price of the bond at the beginning of the year: Rs. 90
Price of the bond at the end of the year: Rs. 95.40
Interest received for the year: Rs. 13.50
The rate of return can be computed as follows:
13.50 + (95.40-90) / 90 = 0.21 or 21% per annum
the return of 21% consist of 15% current yield and 6% capital gain yield.
There is always a direct association between the rates of return and the asset prices. Finance theory stipulates that the price of any asset is equal to the sum of the discounted cash flows which the capital asset owner would receive. Accordingly, the current price of any capital asset can be expected, symbolically, as
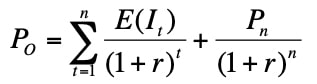
……………….. (Eqn 3)
Where E (Rt ) = expected income to be received in year ‘t’
PO = Current price of the capital asset
Pn = Price of the asset on redemption or on liquidation
R = The rate of return investors expect given the risk inherent in that capital asset.
Thus, ‘r’ is the rate or return, which the investors require in order to invest in a capital asset, that is used to discount the expected future cash flows from that capital asset.
Risk-Return Relationship
The most fundamental tenet of Finance Literature is that there is a trade-off between risk and return. The risk-return relationship requires that the return on security should be commensurate with its riskiness. If the capital markets are efficient operationally then all investment assets should provide a rate or return that is consistent with the risks associated with them. The Risk and return are directly variable. i.e., an investment with higher risk should produce a higher return.
The risk/return trade-off could easily be called the “ability-to-sleep-at-night test.” While some people can handle the equivalent of financial skydiving without batting an eye, others are terrified to climb the financial ladder without a secure harness. Deciding what amount of risk you can take while remaining comfortable with your investments is very important.
In the investing world, the dictionary definition of risk is the chance that an investment’s actual return will be different than expected. Technically, this is measured in statistics by standard deviation. Risk means you have the possibility of losing some, or even all, of our original investment.
Low levels of uncertainty (low risk) are associated with low potential returns. High levels of uncertainty (high risk) are associated with high potential returns. The risk/ return trade-off is the balance between the desire for the lowest possible risk and the highest possible return. This is demonstrated graphically in the chart below. A higher standard deviation means a higher risk and higher possible return.
A common misconception is that higher risk equals greater return. The risk/return trade-off tells us that the higher risk gives us the possibility of higher returns. There are no guarantees. Just as risk means higher potential returns, it also means higher potential losses.
On the lower end of the scale, the risk-free rate of return is represented by the return on the Treasury Bill of Government Securities because their chance of default is next to nothing. If the risk-free rate is currently 8 to 10%, this means, with virtually no risk, we can earn 8 to 10% per year on our money.
The common question arises: who wants to earn 6% when index funds average 12% per year over the long run? The answer to this is that even the entire market (represented by the index fund) carries risk. The return on index funds is not 12% every year, but rather–5% one year, 25% the next year, and so on. An investor still faces substantially greater risk and volatility to get an overall return that is higher than predictable government security. We call this additional return the risk premium, which in this case is 8% (12% – 8%).
Determining what risk level is most appropriate for you isn’t an easy question to answer. Risk tolerance differs from person to person. Your decision will depend on your goals, income and personal situation, among other factors.
The portfolio analysis begins where the security analysis ends and this facts has important consequences for investors. Portfolios, which are combinations of securities, may or may not take on the aggregate characteristics of their individual parts
Portfolio analysis considers the determination of future risk and return in holding various blends of individual securities. Portfolio expected return is a weighted average of the expected return of individual securities but portfolio variance, in sharp contrast, can be something less than a weighted average of security variances.
As a result an investor can than any other security in the portfolio. This seemingly curious result occurs because risk depends greatly on the covariance among returns of individual securities. We will show how an investor can reduce expected risk through diversification, why this risk reduction and expected risk level of a given portfolio of assets.
Read More Articles