Introduction to Bond Valuation
Fixed-income financial instruments which, traditionally, have been identified as a long-term source of funds for a corporate enterprise are the cherished conduit for investors’ money. An assured return and a high-interest rate are responsible for the preference of bonds over equities.
The year 1996-97 witnessed hectic trading in the debt market, as resource mobilization reached a record level of almost Rs. 25,000 crores which was much above the equity segment. In the first seven months of the fiscal year 1998-99, the funds mobilized by ICICI (Four debt issues) and IDBI have accounted for 90 percent of Rs. 3,175 crores mopped in the primary market.
Financial institutions, banks and corporate bodies are offering attractive bonds like retirement bonds, education bonds, deep discount bonds, encash bonds, money multiplier bonds and index bonds. Knowing how to value fixed income securities (bonds) is important both for investors and managers. Such knowledge is helpful to the former in deciding whether they should buy or sell or hold securities at prices prevailing in the market.
Table of Contents
Bond Valuation Terminology
Bond
A long-term debt instrument (a legal contract) in which a borrower agrees to make payments of principal and interest, on specific dates, to the holders of the bond. A bond or debenture is a debt instrument issued by the government or a government agency or a business enterprise. Table 1 describes briefly the variety of debt instruments in the Indian market.
| Type | Typical Features |
|---|---|
| Central Government Securities | Medium-to long-term bonds issued by RBI on behalf of GOI. Coupon payments are semi-annual. |
| State Government Securities | Medium-to long-term bonds issued by RBI on behalf of the state government. Coupon payments are semi-annual. |
| Government Guaranteed Bonds | Medium-to long-term bonds issued by government agencies and guaranteed by the central government or a state government. Coupon payments are semi-annual. |
| PSU Bonds | Medium- to long-term bonds issued by public sector companies in which the central or state government has an equity stake of 51 percent or more. |
| Corporate Debentures | Short-to medium-term debt issued by private and public sector companies. |
| Money Market Instruments | Debt instruments like Treasury Bills (issued by GOI), Commercial Paper (issued by corporates) and Certificates of deposits (issued by banks and financial institutions) that have a maturity of less than a year. |
In order to understand the valuation of bonds, we need to be familiar with certain bond-related terms.
Par Value
It is the value stated on the face of the bond. It represents the amount the firm borrows and promises to repay at the time of maturity. Usually, the par or face value of bonds issued by business firms is Rs. 100. Sometimes it can be Rs. 1000.
Coupon Rate and Interest
A bond carries a specific interest rate which is called the coupon rate. The interest payable to the bondholder is simply par value of the bond × coupon rate. Most bonds pay interest semi-annually.
For example, a GOI security which has a par value of Rs. 1000 and a coupon rate of 11 percent pays an interest of Rs. 55 every six months.
Maturity Period
Typically, bonds have a maturity period of 1-10 years; sometimes they have a longer maturity. At the time of maturity, the par (face) value plus perhaps a nominal premium is payable to the bondholder.
Concept of Value
- Book Value: Book value per share is determined as net worth divided by the number of shares outstanding. Book value reflects historical cost, rather than value.
- Replacement Value: Replacement value is the amount that a company would be required to spend if it were to replace its existing assets in the current condition.
- Liquidation Value: Liquidation value is the amount that a company could realise if it sold its assets, after having terminated its business.
- Going Concern Value: Going concern value is the amount that a company could realise if it sold its business as an operating business.
- Market Value: Market value of an asset or security is the current price at which the asset or the security is being sold or bought in the market.
Time Value Concept
The time value concept of money is that the rupee received today is more valuable than a rupee received tomorrow.
The time value of money makes the rupee invested today to grow more than a rupee in the future. To quantify this concept mathematically compounding and discounting principles are used.
The one period future time value of money is given by the equation:
Future Value = Present Value (1 + interest rate). If hundred rupees are put in a savings bank account in a bank for one year, the future value of money will be:
Future Value = Rs. 100 (1.0 + 6%) 100 × 1.06 = Rs. 106.
If the deposited money is allowed to cumulate for more than one time, the period exponent is added to the previous equation.
Future Value = (Present Value) (1 + Interest Rate)t
Investment Management 1-8 final modified.pmd
t: the number of time periods the deposited money accumulates as interest.
Example: Suppose Rs. 100 is put for two years at the 6% rate of interest, money will grow to be Rs. 112.36.
Future Value = Present value (1 + interest rate)2 = 100 (1 + 0.06)2
= 100 (1.1236)
= 112.36
Present Value
The present value of money can be found simply by reversing the earlier equation.
Present value = (Future value) / (1 + interest rate)
Example: Here, the discounting principle is used. Today’s worth of Rs. 100 to be received after a year at 10 percent interest would be:
= 100 / 1+ 0.10
= 100/1.1
= 90.90
The multiple period of present value equation takes into account of the multiple periods.
Present value = (Future value) / (1 + interest rate)t
Bond Valuation Model
The value of a bond- or any asset, real or financial- is equal to the present value of the cash flows expected from it. Hence, determining the value of a bond requires:
- An estimate of expected cash flows
- An estimate of the required return
To simplify the analysis of bond valuation we will make the following assumptions:
- The coupon interest rate is fixed for the term of the bond.
- The coupon payments are made every year and the next coupon payment is receivable exactly a year from now.
- The bond will be redeemed at par on maturity.
Given these assumptions, the cash flow for a non-callable bond comprises an annuity of a fixed coupon interest payable annually and the principal amount payable at maturity. Hence the value of a bond is:
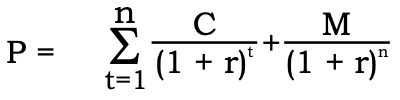
Where,
P = value (in rupees)
n = number of years
C = annual coupon payment (in rupees)
r = periodic required return
M = maturity value
t = time period when the payment is received.
Since the stream of semi-annual coupon payments is an ordinary annuity, we can apply the formula for the present value of an ordinary annuity.
Hence the bond value is given by the formula:
P = C × PVIFAr, n, n + M × PVIFr, n
To illustrate how to compute the value of a bond, consider a 10-year, 12 percent coupon bond with a par value of Rs. 1000. Let us assume that the required yield on this bond is 13 percent. The cash flows for this bond are as follows:
- 10 annual coupon payments of Rs. 120.
- Rs. 1000 principal repayment 10 years from now.
The value of the bond is:
P = 120 × PVIFA13%, 10 Year + 1,000 × PVIF13%, 10 Year
= 120 × 5.426 + 1000 × 0.295
= 651.1 + 295 = Rs. 946.1
Bond values with semi-annual interest
Most bonds pay interest semi-annually. To value such bonds, we have to work with a unit period of six months, and not one year. This means that the bond valuation equation has to be modified along the following lines:
- The annual interest payment, C, must be divided by 2 to obtain the semi-annual interest payment.
- The number of years to maturity must be multiplied by two to get the number of half-yearly periods.
- The discount rate has to be divided by two to get the discount rate applicable to half-yearly periods.
- With the above modifications, the basic bond valuation becomes:
P = C/2 (PVIFAr/2, 2n) + M (PVIFr/2, 2n)
where,
P = value of the bond
C/2 = semi-annual interest payment
R/2 = discount rate applicable to a half-year period
M = maturity value
2n = maturity period expressed in terms of half-yearly periods.
Bond Yield
Bond yield is the return an investor realizes on a bond. The bond yield can be defined in different ways. Setting the bond yield equal to its coupon rate is the simplest definition. The current yield is a function of the bond’s price and its coupon or interest payment, which will be more accurate than the coupon yield if the price of the bond is different than its face value. More complex calculations of a bond’s yield will account for the time value of money and compounding interest payments.
The bond yield is the annualized return of the bond. Thus, bond yield will depend on the purchase price of the bond, its stated interest rate — which is equal to the annual payments by the issuer to the bondholder divided by the par value of the bond — plus the amount paid at maturity.
Let us discuss the bond yields in the following ways:
The current yield
The current yield is the coupon payment as a percentage of current market prices. Because bonds trade in the secondary market, they may sell for less or more than par value, which will yield an interest rate that is different from the nominal yield, called the current yield, or current return.
Since the price of bonds moves in the opposite direction of interest rates, bond prices decrease when interest rates increase, and vice versa.
Current yield = Annual coupon payment / Current market price
With this measure the investors can find out the rate of cashflow from their investments every year. The current yield differs from the coupon rate, since the market price differs from the face value of the bond. When the bond’s face value and market price are same, the coupon rate and the current yield would be the same. For example, when the coupon payment is 8% for Rs. 100 bond with the same market price, the current yield is 8%. If the current market price is Rs. 80 then the current yield would be 10%.
Yield to Maturity (YTM)
The concept of yield-to-maturity (YTM) is one of the widely used tools in bond investment management. Arithmetically, YTM is the single discount factor that makes present value of future cashflows from a bond equal to the current price of the bond. Intuitively, YTM is the rate of return, which an investor can expect to earn if the bond is held till maturity.
The yield to maturity is calculated based on certain assumptions. They are:
- There should not be any default. Coupon and principal amount should be paid as per schedule.
- The investor has to hold the bond till maturity.
- All the coupon payments should be reinvested immediately at the same interest rate as the same yield to maturity of the bond.
Understanding this, is crucial for better investment decisions. For example, if an 11 per cent coupon paying bond with four years to mature has a TYM, of say 13 percent it would be realised only if two conditions are met:
One, the bond is held till maturity (for four years), and two, the interest received from the bond is reinvested for the rest of the period at 13 per cent. Otherwise actual or realised rate of return of the investor will be different from the expected return.
In the above example, if coupon receipts are re-invested at say, 10 per cent for the rest of the period then the realised rate of return will be less than the YTM. Conversely, if the coupon receipts are reinvested at 14 per cent, the realised rate of return will be higher than the YTM.
Any difference in the re-investment rate will cause a difference between the actual return and the YTM. In this sense, the YTM is only a measure of yield. It cannot be regarded as a measure of return from a coupon-paying bond.
Zero Coupon Bonds
The YTM concept has a slightly different meaning for Zero Coupon Bonds (ZCB), popularly known as Deep Discount Bonds (DDB). ZCBs do not carry any coupon but are issued at a price discounted to the face value. On maturity, these bonds are redeemed at face value. Since thee bonds do not have any coupon payments during the life of the bond, the question of re-investment of coupon payments does nto arise at all. There is no re- investment risk for ZCBs.
To find out the yield to maturity the present value technique is adopted. The formula is,
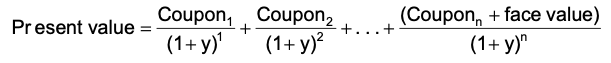
Y = The yield to maturity.
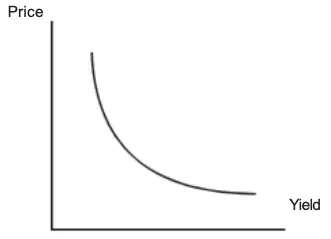
Price Yield Relationship
A basic property of a bond is that its price varies inversely with yield. The reason is simple. As the required yield increases, the present value of the cash flow decreases; hence the price decreases.
Conversely, when the required yield decreases, the present value of the cash flow increases; hence the price increases. The graph of the price-yield relationship for any callable bond has a convex shape as shown in Fig
Relationship between Bond Price and Time
Bond prices, generally, change with time as the price of a bond must equal its par value at maturity (assuming that there is no risk of default).
For example, a bond that is redeemable for Rs. 1000 (which is its par value) after 5 years when it matures, will have a price of Rs. 1000 at maturity, no matter what the current price is. If its current price is, say, Rs. 1100, it is said to be a premium bond. If the required yield does not change between now and the maturity date, the premium will decline over time as shown by curve A in Fig 2.
On the other hand, if the bond has a current price of say Rs. 900, it is said to be a discount bond. The discount too will disappear over time as shown by curve B in Fig 2. Only when the current price is equal to par value-in such a case the bond is said to be a par bond-there is no change in price as time passes, assuming that the required yield does not change between now and the maturity date. This is shown by the dashed line in Fig 2.

Relationship between coupon rate, required yield, and price
As yields change in the marketplace, prices of bonds change to reflect the new required yield. When the required its coupon rate, the bond sells at a discount. When the required yield Years to maturity on a bond equals its coupon rate, the bond sells at par. When the required yield on a bond falls below its coupon rate, the bond sells at a premium. We can summarise the relationship between coupon rate, required yield, and price as follows:
Coupon Rate < Required Yield <=> Price < Par (Discount bond)
Coupon Rate = Required Yield <=> Price = Par
Coupon Rate > Required Yield <=> Price > Par (Premium bond)
Realised Yield to Maturity(YTM)
The YTM calculation assumes that the cash flows received through the life of a bond are reinvested at a rate equal to the yield to maturity. This assumption may not be valid as reinvestment rate/s applicable to future cash flows may be different. It is necessary to define the future reinvestment rates and figure out the realised yield to maturity.
Bond Market
Bonds are bought and sold in large quantities. Most trading in bonds, however, takes place over the counter. This means that the transactions are privately negotiated and they do not take place through the process of matching of orders on an organised exchange. This is a characteristic of bond markets all over the world, not just in India. Because the bond market is largely over the counter, it lacks transparency. A financial market is transparent if you can easily observe its prices and volumes.
The National Stock Exchange has a Wholesale Debt Market (WDM) segment. The WDM segment is a market for high value transactions in government securities, PSU bonds, commercial papers, and other debt instruments. The quotations of this segment mostly reflect over-the-counter transactions that are privately negotiated over the phone or computer and registered with the exchange for reporting purposes.
Read More Articles